Photonics Lab Instructional Videos


Please Wait
Photonics How-To Videos Providing Insights Into Getting Things Done in the Lab
Sometimes the best way to learn is by watching someone else. Thorlabs offers these videos to share tips, tricks, and methods we find ourselves frequently using in the lab. If you have any questions, please contact Tech Support.
Laser Alignment and Setup:
- How to Align a Laser
- Align Fiber Collimators to Create Free Space Between Single Mode Fibers
- Setting Up a TO Can Laser Diode (Viewer Inspired)
- Setting up a Pigtailed Butterfly Laser Diode (Viewer Inspired)
Polarization:
- Align a Linear Polarizer's Axis to be Vertical or Horizontal to the Table
- Align a Linear Polarizer 45° to the Plane of Incidence
- Create Circularly Polarized Light Using a Quarter-Wave Plate (QWP)
- Distinguish the Fast and Slow Axes of a Quarter-Wave Plate
- Build a Polarimeter to Find Stokes Values, Polarization State (Viewer Inspired)
- New! How Light’s Incident Angle Affects Transmission & Finding Brewster’s Angle
Optics and Optical Devices:
- Build a Solar Imaging Telescope with Tracking Capability
- Collimate a Laser with a Shear-Plate Collimation Tester (Viewer Inspired)
- Use Laser Speckle to Find the Beam Focus
- Optical Power Meter Parameter Setup for Improved Accuracy
- Align an Off-Axis Parabolic (OAP) Mirror to Collimate a Beam (Viewer Inspired)
- Calibrate a Spatial Light Modulator (SLM) for Phase Delay (Viewer Inspired)
- Herriott Cell Setup and Configuration (Viewer Inspired)
- Collimate Light from an LED
- How to Align an Optical Isolator
Fiber Optics:
- Cleave a Large-Diameter Silica Fiber Using a Hand-Held Scribe
- PM Fiber Measurements Used to Align Incident Polarization State (Viewer Inspired)
- Measure the Insertion Loss of a Fiber Optic Component
- Align FiberPorts on a FiberBench (Viewer Inspired)
Optomech:
- Tips for Bolting Post Holders to Optical Tables, Bases, and Breadboards
- Mounting your Optomech: Bases, Post Holders, and Posts
- How to Motorize a Manual Translation Stage
- Working with KF (QR) Vacuum Flange Components
- Working with CF Vacuum Flanges
Software Tutorials:
- Visual Studio® Project Setup and C# Programming - Kinesis® BBD300 Series
- Raster Scan Using Visual Studio® and C# Programming - Kinesis® BBD300 Series Controller
- Camera Setup and Image Acquisition Using Visual Studio® and C# Programming
- Python® Automation of a Rotation Mount and Power Meter (Viewer Inspired)
Date of Last Release: May 7, 2024
How to Align a Laser
Two methods for aligning a laser beam so that it propagates parallel to the surface of the optical table are demonstrated.
The first technique adjusts the pointing angle of a laser, whose tip and tilt can be adjusted. Using a ruler, the laser beam is leveled and directed along a row of tapped holes in the table.
Starting with this aligned beam, the technique for changing both the direction and the height of a beam from a fixed laser source is demonstrated. Two mirrors, which are set at different heights, direct the beam along another row of tapped holes in the table. The beam is then leveled at the height of the second mirror using two irises.
| Products Featured During Demonstration | ||
| Laser Module | Kinematic Mounts | Irises |
| Adapter (Laser to Mount) | Mirrors | Ruler |
Date of Last Edit: Sept. 8, 2020
|
Right Click to Copy Link to this Section |
1 |
Optical Power Meter Parameter Setup for Improved Accuracy
An optical power meter should be configured specifically for the light incident on the power sensor. Three important optical power meter parameters to set are the center wavelength of the light, the maximum optical power the sensor will measure, and the zero offset resulting from the detection of ambient light.
The procedure for setting these three parameters, and some things to consider while configuring them, are demonstrated and discussed.
Always follow your institution's laser safety guidelines. Unlike the low-power source used in this demonstration, other laser sources may be damaged by back reflections. Many stray reflections, which can endanger colleagues and the laser, can be avoided by blocking the laser beam when it is not needed.
| Products Featured During Demonstration | ||
| Optical Power Meter | Optical Power Sensor | Fiber-Coupled Laser Source |
Date of Last Edit: Sept. 24, 2020
|
Right Click to Copy Link to this Section |
2 |
How to Motorize a Manual Translation Stage
The procedures for replacing the manual adjusters on a couple of translation stages with motorized actuators are demonstrated. Using the techniques described here allows the adjuster to be exchanged without damaging the stage.
The first example uses a MT1B linear translation stage with a 0.5" travel range. The adjuster screw is swapped for a ZFS13B stepper-motor-driven actuator. In the second half of the video, the micrometer on an XR25P linear translation stage with a 1" travel range is replaced by a DC-servo-motor-driven actuator.
In addition, the video provides an introduction to best practices for mounting these stages to a table or breadboard and demonstrates the use of the locking plate.
| Products Featured During First Half of Demonstration | Products Featured During Second Half of Demonstration | |||
| Linear Translation Stage | Stepper-Motor-Driven Actuator | Linear Translation Stage | DC-Servo-Motor-Driven Actuator | |
Date of Last Edit: Nov. 11, 2023
|
Right Click to Copy Link to this Section |
3 |
Tips for Bolting Post Holders to Optical Tables, Bases, and Breadboards
A common, unfortunate result of securing a post holder to a base or optical table is threads poking up through the bottom of the post holder. These exposed threads limit the height adjustment range offered by the post holder. Additional frustrations can result after rotating the post in the post holder, since this can unintentionally screw the post onto the exposed threads.
The solution is to keep screw length in mind when selecting a setscrew or cap screw to secure a post holder. In this video, observe consequences unfold due to threads projecting up from the bottom of the post holder, and learn techniques for overcoming this problem. The options of securing a post holder to a base or directly to the table are also compared.
A sequel to this Video Insight provides tips for using optomechanical components to build a stable foundation under an optical setup, as well as to avoid accidental damage to the components.
| Products Featured During Demonstration | |||||
| Ø1/2" Post Holders | Ø1/2" Posts | Mounting Base | Iris | Cap Screws | Setscrews |
Date of Last Edit: Apr. 28, 2022
|
Right Click to Copy Link to this Section |
4 |
How to Align an Optical Isolator
Align a Faraday isolator to ensure optimal transmission of optical power from the source, as well as effective suppression of reflections traveling back towards the source. Alignment is demonstrated using a polarization-dependent free-space isolator with a 510 nm to 550 nm operating range and a linearly polarized and collimated 520 nm laser.
These optical isolators output linearly polarized light and provide best performance when the input beam is linearly polarized.
Always follow your institution's laser safety guidelines. Unlike the low-power source used in this demonstration, other laser sources may be damaged by back reflections. Many stray reflections, which can endanger colleagues and the laser, can be avoided by blocking the laser beam when it is not needed.
| Products Featured During Demonstration | ||
| Free-Space Isolator | Power Sensor | Post Collar |
| Laser | Power Meter | Balldrivers and Hex Keys |
Date of Last Edit: Sept. 10, 2020
|
Right Click to Copy Link to this Section |
5 |
Align a Linear Polarizer's Axis to be Vertical or Horizontal to the Table
The beam paths through many optical setups are routed parallel to the optical table. When this is the case, both the plane of incidence and the p-polarization state are typically oriented parallel to the table's surface, while the s-polarization state is perpendicular. Therefore, polarizers aligned to pass p- or s- polarized light effectively have their axes aligned to be parallel or perpendicular, respectively, to the table's surface.
A procedure for optically aligning the axis of a polarizer to be perpendicular to the optical table is discussed and demonstrated using optical power readings of light transmitted through the polarizer. Then, three options for aligning the axis of a polarizer to be parallel to the table are outlined. The method of crossed polarizers is demonstrated. Tips and tricks for obtaining more precise measurements are also shared.
| Products Featured During Demonstration | |||
| Collimated Laser | Polarizing Beam Splitter | Optical Power Sensor | Post Collar |
| Linear Polarizers | Precision Rotation Mounts | Power Meter | Ruler |
Date of Last Edit: Oct. 23, 2020
|
Right Click to Copy Link to this Section |
6 |
Cleave a Large-Diameter Silica Fiber Using a Hand-Held Scribe
An optical-quality end face can be achieved when a large-diameter optical fiber is manually cleaved using a hand-held scribe. The procedure is demonstrated using a multimode fiber with a 400 µm diameter core.
After stripping the protective polymer buffer from the end of the fiber and securing the fiber to a flat surface, a hand-held scribe is used to score the top surface of the fiber. The scribe should create a shallow nick in the fiber's cladding, away from the fiber's core. When cleaving smaller-diameter fibers, avoid creating too deep of a nick by reducing the scribing force and sweeping motion. In some cases, it is sufficient to lightly press a stationary scribe to the fiber. Applying a longitudinal tension to the fiber, across the nicked region, cleaves the fiber.
Also demonstrated is the visual evaluation of the end face quality using an eye loupe. A good quality end face will be a flat plane, perpendicular to the fiber's long axis. The light output from the cleaved end face was also observed on a viewing screen, and tips are shared for inspecting the output light distribution for information about the quality of the end face.
| Products Featured During Demonstration | ||||
| Fiber Buffer Stripping Tool | Fiber Grippers | Quick-Release Adjustable Fiber Clamp | SMA Bare Fiber Terminator | 10X Eye Loupe |
| Ruby Scribe | Fiber-Coupled LED | Free-Standing Platform | Pillar Posts | Viewing Screen |
Date of Last Edit: Nov. 3, 2020
|
Right Click to Copy Link to this Section |
7 |
Measure the Insertion Loss of a Fiber Optic Component
Insertion loss measures the drop in optical power caused by the addition of a device to a fiber optic network. All sources of optical loss contribute to a device's insertion loss, including reflections, absorption and scattering due to intrinsic material properties, micro- and macrobending losses, split ratios, splice loss, and connector loss.
A single-ended insertion loss measurement is demonstrated. In this approach, a reference cable is attached to the source, and then the power at the cable's output is measured. Next, a mating sleeve is used to attach the component under test to the reference cable. The optical power at the selected output port of the component is measured. The insertion loss is calculated by first taking the ratio of this power reading to the power measured at the reference cable output, and then expressing the ratio in terms of decibels (dB).
The single-ended insertion loss measurement includes the loss from coupling light into the device, which is often mostly due to the misalignment of the fiber cores in the mating sleeve. However, this measurement does not include the same type of loss that occurs when coupling the light output from the device into the next leg of the fiber optic network. Note also that the insertion loss is wavelength dependent and will differ for each combination of device input and output ports selected for the measurement. This is due to the differences in split ratio, bend loss, absorption, scattering, reflections, and all other individual sources of attenuation along the optical path between the two ports.
| Products Featured During Demonstration | |||||
| Fiber-Coupled Laser Source | Mating Sleeve | Power Sensor | Power Meter | 50:50 Coupler | Single Mode Patch Cables |
Date of Last Edit: Dec. 3, 2020
|
Right Click to Copy Link to this Section |
8 |
Create Circularly Polarized Light Using a Quarter-Wave Plate (QWP)
Circularly polarized light can be generated by placing a quarter-wave plate in a linearly polarized beam, provided a couple of conditions are met. The first is that the light's wavelength falls within the wave plate's operating range. The second is that the wave plate's slow and fast axes, which are orthogonal, are oriented at 45° to the direction of the linear polarization state. When this is true, the incident light has equal-magnitude components parallel to the wave plate's two axes. The wave plate delays the component parallel to the slow axis by a quarter of the light's wavelength (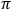 /2) with respect to the component parallel to the fast axis. By creating this delay, the wave plate converts the polarization state from linear to circular.
/2) with respect to the component parallel to the fast axis. By creating this delay, the wave plate converts the polarization state from linear to circular.
An animation at the beginning of the demonstration illustrates the results of aligning the input linear polarization state with the wave plate's fast axis, slow axis, and angles in between. The perspective used to describe the angles and orientations is looking into the source, opposite the direction of light propagation. The procedure is then demonstrated for orienting input and output polarizers to define the reference orthogonal polarization directions, as well as provide polarization-dependent power measurements. The wave plate is placed between the two polarizers, and the effects of different orientations are explored. The quality of the circularly polarized light output by the wave plate is checked by rotating the second polarizer's transmission axis. The light's polarization is closer to circular when the power reading fluctuates less during rotation.
| Products Featured During Demonstration | ||||
| HeNe Laser | Quarter-Wave Plate | Precision Rotation Mounts | Power Sensor | Power Meter |
| Optical Isolator (for HeNe) | Linear Film Polarizers | V-Clamp Mount | SM1 Thread Adapter (for Power Sensor) | SM1 Lens Tube |
Date of Last Edit: Dec. 30, 2020
|
Right Click to Copy Link to this Section |
9 |
Align a Linear Polarizer 45° to the Plane of Incidence
The transmission axis of a linear polarizer can be set at a 45° angle to the plane of incidence, with the help of two additional linear polarizers. The two supporting polarizers are aligned so that one's axis is parallel and the other's is perpendicular to the plane of incidence. Orienting the transmission axis of the third polarizer at a 45° angle to the plane of incidence is done by rotating the transmission axis to make 45° angle with the axes of the polarizer pair.
This is demonstrated for the case in which the plane of incidence is parallel to the optical table. The procedure used to align the first polarizer's axis parallel to the table requires repeatedly rotating the polarizer 180° around the vertical axis. The linear polarizer assemblies have rectangular bases, and the fixed position retainer (fork) provides a fixed corner reference on the table. The fork allows the polarizer assembly to be quickly and precisely placed after flipping it around the vertical axis. Following each 180° flip, the transmission axis of the polarizer is first rotated by hand and then finely tuned using the mount's integrated micrometer (mic). After the first polarizer's axis is aligned, the second polarizer's axis is then crossed with it. When this is done, the light transmitted by the second polarizer is minimized.
The third polarizer is then placed between the other two polarizers and its transmission axis is rotated. The rotation angle affects the optical power transmitted by this set of three polarizers, and the throughput is maximized when the angle is 45° with the plane of incidence. One way to check the result, as well as determine the maximum possible power that can be obtained at the detector, is to use the cosine squared (Malus') law. It calculates the power output by a linear polarizer when the incident light is linearly polarized.
| Products Featured During Demonstration | |||
| Laser Module | Precision Rotation Mounts | Power Sensor | Power Meter |
| Linear Film Polarizers | Fixed Position Retainer (Fork) | SM1 Thread Adapter (for Power Sensor) |
SM1 Lens Tube |
Date of Last Edit: Jan. 19, 2024
|
Right Click to Copy Link to this Section |
10 |
Align Fiber Collimators to Create Free Space Between Single Mode Fibers
Two collimators, inserted into a fiber optic setup, provide free-space access to the beam. The first collimator accepts the highly diverging light from the first fiber and outputs a free-space beam, which propagates with an approximately constant diameter to the second collimator. The second collimator accepts the free-space beam and couples that light into the second fiber. Some collimation packages, including the pair used in this demonstration, are designed for use with optical fibers and mate directly to fiber connectors.
Ideally, 100% of the light emitted by the first fiber would be coupled into the second fiber, but some light will always be lost due to reflections, scattering, absorption, and misalignment. Misalignment, typically the largest source of loss, can be minimized using the alignment and stabilization techniques described in this video.
In this demonstration, the first fiber is single mode. The optical power incident on the second collimator, as well as the power output by the second fiber, are measured. When the second fiber is multimode with a 50 µm diameter core, alignment resulted in 91% of the power incident on the second collimator being measured at the fiber output. This value was 86% when the second fiber is single mode. Some differences in collimator designs, and their effects on the characteristics of the collimated beams, are also discussed.
| Products Featured During Demonstration | ||||
| Fiber-Coupled Laser | Kinematic Mounts | Fiber Adapter Cap (for Power Sensor) |
Single Mode Patch Cable (FC/PC) | Fiber Cable Storage Reels |
| Triplet Fiber Optic Collimators | Power Sensor | Power Meter | Hybrid Single Mode Patch Cable | 2" Posts |
| Adapter (Mount-to-Collimator) |
SM1 Thread Adapter (for Power Sensor) |
Fiber Connector Cleaner | Step-Index Multimode Patch Cable | 0.5" Post Holders |
Date of Last Edit: April 1, 2021
|
Right Click to Copy Link to this Section |
11 |
Setting Up a TO Can Laser Diode (Viewer Inspired)
Installing a TO can laser diode in a mount and setting it up to run under temperature and current control presents many opportunities to make a mistake that could damage or destroy the laser. This step-by-step guide includes tips for keeping humans and laser diodes safe from harm.
Protection from the considerable risk of electrostatic discharge (ESD) is provided by an ESD strap, but only if the strap is grounded and worn correctly. Wearing the strap as demonstrated makes it easier to keep the strap's metal plate in constant skin contact. Moisturizing the skin with lotion formulated for use in electronic and cleanroom environments can also help.
A laser diode can be damaged by attempting to force it into a socket that is the wrong size. To avoid this, find a suitable mount by referencing the physical dimensions of the pins identified in the video. Since current flow in the wrong direction is also dangerous to laser diodes, it is critical to correctly orient the laser in the socket, as well as properly set the polarity of the mount's switches. Current drivers typically also have a polarity setting. The diode orientation and mount and driver settings can be determined using information included in the laser's pin diagram and electrical diagram, whose symbols are decoded and explained in the video.
Excessive operating temperatures and drive current are both risks that can be mitigated using correctly configured current and temperature controllers. Their setup is demonstrated. The proper use of two frequently misunderstood parameters, maximum power and maximum current, in configuring the current driver is also shown.
| Products Featured During Demonstration | ||||
| TO Can Laser Diode | ESD Strap | Current Controller | Integrating Sphere Power Sensor | Flexure Clamping Base |
| Laser Diode Mount | Laser Safety Glasses | Temperature Controller | Power Meter | Tweezers |
Date of Last Edit: May 7, 2021
|
Right Click to Copy Link to this Section |
12 |
Setting Up a Pigtailed Butterfly Laser Diode (Viewer Inspired)
A laser diode packaged in a butterfly housing can be precisely controlled, in a compact package, when the laser is installed in a mount that includes thermoelectric cooler (TEC) and current drivers. The mount can make it easier, and safer, to operate the laser, but the procedure for installing the laser in the mount and configuring the settings requires some care. This video provides a step-by-step guide, which begins with an introduction to the different components and concludes with the laser operating under TEC control and with the recommended maximum current limit enabled.
This demonstration is also filled with useful details that can be forgotten in bulleted lists describing the setup procedure. These include tips for wearing an ESD strap, determining when to use thermal grease, applying the right amount of thermal grease, creating good electrical connections between the laser's pins and mount, easing the removal of the laser from the mount, safeguarding the fiber pigtail of the installed laser, cleaning an angled physical contact (APC) fiber connector, using the Steinhart-Hart thermistor values provided on the laser spec sheet, and making power measurements to determine the laser's current limit setting.
Date of Last Edit: June 17, 2021
|
Right Click to Copy Link to this Section |
13 |
Distinguish the Fast and Slow Axes of a Quarter-Wave Plate
A wave plate has two axes, and light polarized parallel to the slow axis is delayed more than light polarized parallel to the orthogonal fast axis. The wave plate's retardance determines the delay difference. A couple of crossed polarizers can be used to locate an axis (Video Insight) but cannot identify the axis as fast or slow. However, by including a mirror in the setup and comparing optical power measurements with calculated values, it is possible to distinguish between the fast and slow axes of a quarter-wave plate. Note that this technique cannot be used to distinguish the fast and slow axes of a half-wave plate.
The video includes an overview of the measurement setup and discussion of the conventions used to align and orient the optical components. The accurate interpretation of the results depends on these details, including whether the transmission axes of the generating and analyzing polarizers are parallel or orthogonal (crossed). Crossed polarizers are used in this demonstration, in contrast to a paper [1] that also describes the technique.
The fast and slow axes of the quarter-wave plate are identified by comparing measurements of the power transmitted through the system to a pair of theoretical curves. The Fresnel reflection equations, as well as other equations, needed to compute these curves are provided. The refractive index of the reflective surface is required to generate these curves. Be aware that complex refractive indices can be written with a positive or a negative sign before the imaginary part, depending on the preferred convention. While either option is compatible with this approach, the chosen sign affects the interpretation of the curves. In this demonstration, the positive-sign convention was chosen.
| Products Featured During Demonstration | ||||
| HeNe Laser | Quarter-Wave Plate | Unprotected Gold Mirror | Power Sensor | Power Meter |
| Optical Isolator (for HeNe) | Linear Polarizers | Kinematic Mirror Mount | SM1 Thread Adapter (for Power Sensor) |
SM1 Lens Tube |
| V-Clamp Mount | Precision Rotation Mounts | Iris | Balldrivers | Quick-Release Lens Tube Adapter |
[1] Petre C t
t lin Logof
lin Logof tu, "Simple method for determining the fast axis of a wave plate," Opt. Eng. 44, 3316-3318 (2002).
tu, "Simple method for determining the fast axis of a wave plate," Opt. Eng. 44, 3316-3318 (2002).
Date of Last Edit: Mar. 25, 2022
|
Right Click to Copy Link to this Section |
14 |
Visual Studio® Project Setup and C# Programming - Kinesis® BBD300 Series Controller
Starting a program and initializing connected devices can be one of the largest hurdles to writing code that remotely controls a device. This tutorial for Thorlabs' Kinesis® software package provides step-by-step instructions for using C# and the .NET framework to create a new Visual Studio® project and initialize connected devices, which in this case is a BBD300 series motor controller connected to a two-axis stage. A basic move sequence is then added to the program and used to test the execution of the code.
The demonstration begins with instructions for creating a new Visual Studio project and adding the required dynamic link libraries (DLLs). In this example, there is one connected controller. The program is written to execute its two-step initialization process, since the controller's chassis and channels must be initialized individually. Each channel connects to one axis of a connected stage.
In this demonstration, one of the controller's two channels is initialized, allowing the two-axis stage to be moved in one direction. Custom velocity and position settings are specified for the move command, and instructions are included to perform the disconnect shutdown sequence after the move sequence is completed. Try-catch blocks are added to the code to provide instructions to the program in the case that an error is thrown by a method. Command and position status information is made available to the user, and status messages are printed to the PC's console screen.
These steps are used as the foundation of a program described in another Video Insight that executes a stepped, bidirectional raster scan using the same controller and XY stage. The code demonstrated during this video can be downloaded from Thorlabs' official GitHub account.
| Products Featured During Demonstration | |||
| Kinesis Software Package | Two-Axis Brushless DC Controller | XY Scanning Stage | Slide / Petri Dish Holder for Inverted Microscopes |
Date of Last Edit: Nov. 17, 2021
|
Right Click to Copy Link to this Section |
15 |
Build a Polarimeter to Find Stokes Values, Polarization State (Viewer Inspired)
A polarimeter, which is an optical tool used to measure the polarization state of light, can be constructed using linear polarizers, a quarter-wave plate, and an optical power sensor and meter. This video describes two methods for building a manual polarimeter, the classical method and the rotating wave plate method, and then uses both to measure a laser beam's polarization state. [1] Both approaches provide measurement data that describe the polarization state in terms of the four Stokes parameters. This demonstration includes discussion of the relationships between the Stokes parameters and different polarization states, including linearly and circularly polarized light.
In this demonstration, polarization handedness is defined with respect to time and from a perspective of looking into the beam, back towards the source. This video illustrates this convention by visualizing a fixed viewing plane oriented perpendicular to the propagating beam. As the beam passes through the plane, the beam's instantaneous polarization vector traces out a shape on the plane. The shape is traced out as a function of time, and the direction in which the shape is traced corresponds to the handedness of the light. The shape itself is the polarization ellipse, which is a convenient and common way to describe light's polarization state. The relationship between the polarization ellipse and the Stokes parameters is also discussed.
Prior to filming, the transmission axes of the linear polarizers and wave plate used to build these polarimeters were oriented with respect to the table. The following descriptions link to Video Insights demonstrating the alignment procedures:
- Align a linear polarizer horizonal or vertical with respect to the table.
- Align a linear polarizer at 45° with respect to the table.
- Align a wave plate's axis to be horizontal with respect to the table.
- Determine whether a wave plate's axis is fast or slow.
| Products Featured During Demonstration | ||||
| HeNe Laser | Quarter-Wave Plate | Power Sensor | Power Meter | Fixed Position Retainer (Fork) |
| Optical Isolator (for HeNe) | Linear Polarizers | SM1 Thread Adapter (for Power Sensor) |
SM1 Lens Tube | Optical Post Assemblies |
| V-Clamp Mount | Precision Rotation Mounts | Iris | Quick-Release Lens Tube Adapter | Balldrivers |
[1] Beth Schaefer, Edward Collett, Robert Smyth, Daniel Barrett, and Beth Fraher "Measuring the Stokes polarization parameters," Am. J. Phys. 75, 163-168 (2007).
Date of Last Edit: Oct. 19, 2021
|
Right Click to Copy Link to this Section |
16 |
Raster Scan Using Visual Studio® and C# Programming - Kinesis® BBD300 Series Controller
A benefit of motorized XY stages is that they can be remotely controlled to execute a patterned scan, such as a raster scan, across a specified area. This tutorial for Thorlabs' Kinesis® software package provides step-by-step instructions for writing a program for a BBD300-series motor controller that moves the connected two-axis stage in a stepped, bidirectional raster scan pattern. The program is written using C#, the .NET framework, and the Visual Studio® development environment.
This tutorial builds on the foundation established by the previously released Video Insight, Visual Studio Project Setup and C# Programming - Kinesis BBD300 Series Controller. After providing a brief overview of different raster scan patterns and approaches, this demonstration quickly reviews some of the steps included in the Visual Studio Project Setup tutorial. This includes referencing libraries, configuring the project platform, and initializing the controller's chassis and two channels.
Three types of move methods are implemented. One is used to home a chosen stage axis, and another is used to move the stage to a specific position. The third implements a jog, which moves the stage along a particular axis by a specified step size. The raster scan is implemented by first moving the stage to an initial position, and then executing a series of jogs along the stage's X- and Y-axes. An example of debugging the code is shown, and the stepped, bidirectional raster scan is successfully executed.
The code demonstrated during this video can be downloaded from Thorlabs' official GitHub account.
| Products Featured During Demonstration | |||
| Kinesis Software Package | Two-Axis Brushless DC Controller | XY Scanning Stage | Slide / Petri Dish Holder for Inverted Microscopes |
Date of Last Edit: Nov. 17, 2021
|
Right Click to Copy Link to this Section |
17 |
Align an Off-Axis Parabolic (OAP) Mirror to Collimate a Beam (Viewer Inspired)
Off-Axis parabolic (OAP) mirrors are often used to collimate divergent beams, but aligning these mirrors can be a frustrating experience. This is because there are multiple variables that must be controlled during the alignment process. This demonstration divides the procedure into discrete steps and includes helpful tips for successfully positioning the mirror and light source. In addition, the dependence of the correct alignment on the mirror's geometry is discussed, and the typical effects of different misalignment geometries on the beam shape are shown on a viewing screen.
In this demonstration, the divergent output of an optical fiber and an OAP mirror are aligned so that the incident light and the collimated reflected beam travel in a plane parallel to the surface of the optical table. Because of this, an important initial step in the procedure is to set both the height of the source and the center of the mirror mount's bore at the height of the desired collimated beam. Then, an iterative approach is used in which the mirror is rotated to bring the plane of reflection parallel to the plane of the table, and the fiber's end face is moved to the mirror's focal point.
| Key Components | Additional Products Featured During Demonstration | ||||
| Aluminum OAP Mirror | Post Collars | SMA-SMA Patch Cable | Viewing Screen (Smaller) | Spanner Wrench | |
| SM1-Threaded Adapter (for OAP Mirror) |
Fiber-Coupled LED | Lens Mount | Viewing Screen (Larger) | Magnetic Button Clamps | |
| SM1-Threaded Mirror Mount | T-cube LED Driver | SM1-Threaded Fiber Adapter | Ruler | 1/4"-20 Cap Screw Kit | |
Date of Last Edit: Dec. 14, 2021
|
Right Click to Copy Link to this Section |
18 |
Camera Setup and Image Acquisition Using Visual Studio® and C# Programming
When a scientific camera is integrated into a setup, it can be convenient to automate image acquisition and storage using a hardware trigger. This can be enabled using the software development kit (SDK) provided with Thorlabs' scientific cameras. The use of the SDK to control the operation of a scientific camera is demonstrated using a custom Visual Studio® console application written in C#, as well as a setup that includes a scientific camera, light emitting diode (LED), LED driver, and PC.
The demonstration begins with a general overview of the setup, and then steps through the settings needed to configure the LED driver to pulse the LED five times while providing a TTL output signal each time. Pulsing the light source is one approach to limiting a sample's total light exposure, and the TTL signal can be used to synchronize image acquisition with the illumination of the sample. A cable couples the TTL hardware trigger to the camera.
A blank Visual Studio console application is then opened, and the code is explained as it is typed line-by-line. The program finds all available cameras connected to the PC and is used to select one, whose parameters the program will configure for the setup. The exposure time is set to be slightly less than the LED pulse duration, and a single image acquisition is specified to occur when a hardware trigger is received. Each image is saved to a file as a bitmap, and the total number of acquired images is limited to five. The demonstration concludes with the successful execution of the program, which results in five saved image files that were each taken during a separate flash of the LED.
The code demonstrated during this video can be downloaded from Thorlabs' official GitHub account.
File Paths to DLLs and Supporting Documentation:
- Location of DLLs added during project setup: C:\Program Files\Thorlabs\Scientific Imaging\Scientific Camera Support\Scientific Camera Interfaces
- Detailed documention including camera's supported features: C:\Program Files\Thorlabs\Scientific Imaging\Documentation\Scientific Camera Documents
Date of Last Edit: Jan. 24, 2022
|
Right Click to Copy Link to this Section |
19 |
Align FiberPorts on a FiberBench (Viewer Inspired)
This video demonstrates a complete procedure for aligning two FiberPorts on a FiberBench. The procedure takes into account the coupled functionality of the various adjustment screws, such as the Zθ screws. Adjusting any of the three Zθ screws individually affects both the angular orientation and Z-axis position of the lens. When all three Zθ screws are adjusted as a set, it is possible to move the lens such that the final position corresponds to only a change in angular orientation or shift in position along the Z-axis.
For example, adjusting each of the three Zθ screws by the exact same amount in the same direction translates the lens along the Z-axis without affecting the lens's angular orientation. The different techniques used to complete this and other adjustments are shown during the demonstration, so that this alignment procedure can be customized according to preference.
Before aligning the FiberPorts to one another, the lens in each should be pre-aligned to collimate light from a coupled optical fiber. The pre-alignment step should not be necessary if the FiberPort has not been used, since FiberPorts are provided pre-aligned. The alignment procedure begins by tuning the X-axis and Y-axis adjusters and progresses to the Zθ adjusters. To avoid complicating the alignment procedure, it is recommended that the X- and Y-axis adjuster positions are not changed after beginning work with the Zθ adjusters.
The optical power collected by the coupling fiber is used to monitor the progress of the alignment procedure. However, it should be noted that a drop in power after an adjustment may not indicate a misstep in the procedure. Instead, the drop may correspond to a local minimum en route to a global maximum. This demonstration provides tips for interpreting and investigating the progress of the alignment, as well as advice for making consistent adjustments.
| Key Components | Additional Products Featured | ||||
| FiberPorts | SM1 Thread Adapter (for the Power Sensor) |
(FC/PC to FC/PC) |
Fiber Connector Cleaner | ||
| Power Sensor | Adapter Cap |
Single Mode Patch Cable (FC/PC to FC/APC) |
|||
| Irises (Pillar Post and Flexure Clamping Base Used in Free-Standing Iris Assembly) |
Power Meter | Multimode Patch Cable |
Ruler | ||
Date of Last Edit: Feb. 15, 2022
|
Right Click to Copy Link to this Section |
20 |
Working with KF (QR) Vacuum Flange Components
A vacuum connection between two KF flanged components is made by compressing an O-ring between the two flanges. Minimizing leak rates through this vacuum coupling requires the flat flange faces to be smooth and clean, as well as the O-rings to be malleable and undamaged. This video demonstrates methods for coupling and disconnecting KF flanged components and shares tips for handling, maintaining, and assembling these popular vacuum flanges. Vacuum systems that include KF flanges can generally support vacuum levels down to 10-8 Torr (
There are many benefits to using KF flanged components in vacuum systems, including a genderless design, standardized sizes, quick decoupling and reconnection times, and being relatively inexpensive. Many of these features are made possible by the elastomeric O-ring that serves as a gasket.
The effectiveness of the vacuum seal depends on several factors including the conditions of both flange faces and the O-ring, the compression applied to the O-ring, and the O-ring's history of temperature exposure and usage. Excessive amounts of compression (>60%) and exposure to high temperatures increases the rate at which the O-ring develops compression set. Compression set is a term used to refer to permanent changes in the O-ring's shape, which includes stiffening of the elastomeric material. Inspecting the O-ring and flange surfaces as shown in the video, and then replacing damaged components and stiffened O-rings can optimize performance. The application of vacuum grease to an O-ring is also demonstrated, and guidance for determining whether or not to use vacuum grease is provided.
| Products Featured During Demonstration | ||
| Wing Nut Clamp (KF25) | Blank Cap (KF25) | Nitrile Gloves |
| O-Ring and Carrier (KF25) | Elbow and Straight Pipes (KF25) | Solvent Dispenser and Wipes |
Date of Last Edit: June 10, 2022
|
Right Click to Copy Link to this Section |
21 |
Mounting your Optomech: Bases, Post Holders, and Posts
Optical setups are typically built upon a foundation of optomechanical components like posts, post holders, and bases. There are different approaches to designing and building the foundation. Some result in optical setups that are more affected by vibrations and more likely to be misaligned when bumped. In addition, certain techniques used to assemble components can accidentally damage them.
Unfortunately, it is typically necessary to build the entire setup to observe the effects of different approaches, so evaluating the benefits and disadvantages of each can be difficult or time consuming. In addition, the existence of other approaches may not be obvious, since it can be easy to avoid thinking about components that are as familiar as posts, post holders, and bases. The techniques presented in this video are methods we have found useful and should provide a good starting point for working with optomech.
This demonstration shines a spotlight on these common building-block components and includes tips learned though long experience designing and working with them. The purpose and use of features that may have escaped notice, such as the relief cut on bases, the through hole in optical posts, and the benefits of washers are revealed. Guidelines for choosing post and post holder heights to increase mechanical stability are provided, as well as suggestions for avoiding damage to kinematic mounts when attaching a post. This video also demonstrates a potentially unexpected approach for mounting larger components, which uses two post holders, two posts, and a base.
Additional tips for avoiding unintended consequences and preserving the full adjustment height when bolting post holders to optical tables, bases, and breadboards are demonstrated in this Video Insight.
| Products Featured During Demonstration | ||
| Posts | Compact Mirror Mount | 8-32 Hardware Kit Also Available: M4 Hardware Kit |
| Post Holder | Mirror Mount | 1/4"-20 Hardware Kit Also Available: M6 Hardware Kit |
| Mounting Base | Laser Diode Mount | Balldriver Caddy Kit, Imperial Also Available: Balldriver Caddy Kit, Metric |
Date of Last Edit: Apr. 29, 2022
|
Right Click to Copy Link to this Section |
22 |
Use Laser Speckle to Find the Beam Focus
When a lens is mounted in a lens tube, optic mount, or cage plate, the exact position of the lens within the fixture may not be known, which can make it difficult to accurately predict the location of the beam focus and align the system. One approach to finding the beam focus with respect to the fixture uses laser speckle.
During this demonstration, laser speckle is used to find focal points provided by lenses mounted in individual lens tubes. After locating the focus of each mounted lens, the distance between the focal point and the external shoulder of each lens tube is measured.
The mounted lenses are then used to construct a Keplerian beam expander, using a design in which empty lens tubes are inserted between the two mounted lenses. The required total length of the lens tubes separating the two mounted lenses is estimated using the previously measured distances to the focal points. This approach avoids tedious trial-and-error that can result when the beam expander is constructed by first guessing the required total lens tube length, and then iteratively measuring beam quality and adjusting the length until achieving the desired result.
A transmissive glass diffuser is used during this demonstration to create the speckle pattern. The size of the speckle is largest when the ground surface of the diffuser is at the focus, where the beam size is smallest. It is recommended that the beam is incident on the ground face of the diffuser. This allows direct measurement of the distance to the focus, without needing to take the diffuser's optical thickness into account. After assembling the beam expander, a shearing interferometer is used to fine-tune the collimation of the expanded beam.
| Products Featured During Demonstration | |||
| Optical Diffuser | Compact Laser Module | Ø1" Lens Tubes | Dovetail Optical Rail |
| DIY Adapter (Diffuser to Slip-Ring Mount): Lens Tube Coupler and Retaining Ring |
Adapter (Laser to Mount) | Adjustable Ø1" Lens Tubes | Optical Rail Carrier |
| Threaded Kinematic Mount | Slip-Ring Mount | Post Collar | |
| Plano-Convex Lenses | Fiber Storage Reel | Digital Calipers | Ruler |
| Shearing Interferometer | Viewing Screen | Retaining Ring Wrench | V-Groove Block |
Date of Last Edit: June 6, 2022
|
Right Click to Copy Link to this Section |
23 |
Python® Automation of a Power Meter and Rotation Mount (Viewer Inspired)
A Python script that automates control of a Kinesis® K-Cube™ motor controller and a power meter is written using Visual Studio® Code. The program acquires optical power measurements from the power meter as the rotation mount's angle sweeps through 180°, which is required to characterize a variable optical attenuator. Since this code uses libraries developed using the .NET framework, running this code requires Python.NET to be installed.
This tutorial implements the code specific to the K-Cube motor controller first, followed by the code for the power meter. The packages and classes required by both devices are identified, and the steps required to initialize and complete shutdown for both devices are shown. In addition, an approach is described for acquiring power readings and checking controller status while the motor is moving. The Python script is executed once after the K-Cube section of the code is complete, and a second time after the program is finished.
The K-Cube motor controller and power meter were automated in order to characterize the optical power transmitted through a pair of fixed, crossed linear polarizers when a rotating half-wave plate is located between them. As the half-wave plate rotates, the polarization orientation of the light transmitted by the output polarizer remains constant, while the transmitted power varies sinusoidally. Measurements of this transmitted optical power, as well as the corresponding rotation angles of the mount in which the half-wave plate is secured, are provided by the program.
The code written using Visual Studio Code during this video can be downloaded from Thorlabs' official GitHub account.
| Products Featured During Demonstration | ||||
| Motion Control Software | Compact Laser Module | Manual Rotation Mount | Power Sensor | Slip-Ring Mount |
| K-Cube Motor Controller | Adapter (Laser to Mount) | Linear Polarizers | Power Meter | Mounting Base |
| Motorized Rotation Stage | Threaded Kinematic Mount | Wave Plates | Ø1" Lens Tubes | Storage Reel |
Date of Last Edit: Jul. 26, 2022
|
Right Click to Copy Link to this Section |
24 |
Working with CF Vacuum Flanges
A vacuum coupling that supports operation at ultra-high-vacuum levels
Damage to the knife edge, an aggressive approach to tightening the bolts, and reusing gaskets can all result in leaky CF vacuum couplings. The techniques demonstrated in this video reduce the risk presented by these factors, which are all related to the limited malleability of the metal gasket. It is important that the knife edges are in pristine condition, since the gasket is not soft enough to fill narrow or abrupt features, such as a nick in a knife edge. An approach of gradually and iteratively tightening the bolts is effective in maintaining a uniform thickness of the gasket around its circumference, while tightening each bolt all at once can result in thickness variations in the gasket that are difficult or impossible to flatten. This is a consequence of the metal gasket’s limited ability to flow and can result in gaps between the gasket and knife edges. Using a new gasket is always recommended. Even a gasket that was only partially compressed during a previous use may not be malleable enough, when reused, to conform to the contours of the knife edges. This is because compression has the effect of strain (work) hardening the metal.
While a leaky vacuum connection can result in time lost to leak checking and re-opening the vacuum system to locate and fix the problem, productive work can also be delayed as a result of broken or malfunctioning components in or attached to the chamber. Due to this, an overview of special considerations for handling and using fiber feedthroughs is also included in this video.
ConFlat® is a registered trademark of Agilent Technologies, Inc.
| Products Featured During Demonstration | |||
| Optical Fiber Feedthrough | 1/4-Hard Copper Gaskets | Fiber Inspection Scope | Nitrile Gloves |
| UHV Fiber Patch Cable | Solvent Dispenser | Fiber Connector Cleaner | Wipes |
Date of Last Edit: Sept. 20, 2022
|
Right Click to Copy Link to this Section |
25 |
Calibrate a Spatial Light Modulator (SLM) for Phase Delay (Viewer Inspired)
The phase delay (phase modulation) provided by a reflective liquid crystal on silicon spatial light modulator (SLM) depends on a number of things, including the applied control voltage, ambient conditions, and the characteristics of the incident light. When a manufacturer calibrates the SLM’s phase delay as a function of the applied voltage, the calibration is typically performed under specific operating conditions and for collimated light with a particular wavelength and angle of incidence. Since an application’s setup and operating conditions can differ significantly from the manufacturer's, it is often beneficial to recalibrate the SLM’s phase delay for each application.
This Video Insight demonstrates an interferometric method [1] for calibrating the phase delay of reflective SLMs that are designed to modulate the phase without affecting the linear polarization state of the incident light. The calibration setup requires only a collimated, linearly polarized input beam and a camera, in addition to the SLM.
When working with SLMs, it is common to represent phase delay patterns using grayscale values, in which each shade of gray represents a specific phase delay. Calibration determines the specific phase delay provided for each grayscale value, under the current operating conditions. This calibration approach applies a uniform phase delay to one half of the SLM's panel. This half is referred to as the mirror side and provides a reflected beam. A binary phase grating is applied to the other half, which provides a diffracted beam. The reflected and -1st order diffracted beams overlap and create interference fringes, which are monitored during the calibration procedure. The voltage applied to the mirror side of the SLM is varied across the full range, and the fringes shift each time the applied voltage changes. The fringe shift is directly related to the change in phase delay.
A second video made to accompany this Video Insight provides additional background information about the optical properties of the liquid crystal layer. The effects of the applied voltage on the liquid crystal layer’s refractive index are illustrated, as well as the effects of the layer on linearly polarized light with different polarization orientations. Note that the SLM provides unexpected results when the linearly polarized light is not aligned parallel with what is often called the SLM's optic axis, which is actually the rotation plane of the molecules in the liquid crystal layer.
[1] José Luis Martínez Fuentes, et al., "Interferometric method for phase calibration in liquid crystal spatial light modulators using a self-generated diffraction-grating," Opt. Express. 24, 14159 - 14171 (2016).
Date of Last Edit: Nov. 29, 2023
|
Right Click to Copy Link to this Section |
26 |
Collimate a Laser with a Shear-Plate Collimation Tester (Viewer Inspired)
A shear-plate collimation tester is a compact shearing interferometer that is convenient for inserting into a beam path. When in place, the device can be used to test and optimize a laser beam’s collimation. This Video Insight demonstrates a technique for using the device, shares some troubleshooting tips, and provides guidance for determining whether the approach is a good option for testing the collimation of a particular beam.
The device can remain in the beam while the position of the collimating lens, which in this case is an achromatic doublet, is adjusted. Fringes visible on the ground glass diffuser, which is on top of the device, indicate whether the beam is converging, diverging, or collimated.
It should be kept in mind that this technique requires light with sufficient coherence, low wavefront aberrations, and a shear plate thickness compatible with the beam diameter. Note also that the distance over which a beam is collimated is never infinite, so the device should be located within approximately one Rayleigh range of the collimated beam's waist.
Assistance is provided for diagnosing the problem when no interference fringes are visible, or the fringes are difficult to interpret. The demonstration shows when the solution is to use a thinner shear plate, to adjust the lens position, or to add a magnified viewer to the top of the device. It is also shown that a different method is required to test and optimize beam collimation when there are significant wavefront aberrations or an insufficient coherence length.
Date of Last Edit: Mar. 22, 2023
|
Right Click to Copy Link to this Section |
27 |
PM Fiber Measurements Used to Align Incident Polarization State
Polarization-maintaining (PM) fiber can only preserve the polarization state of input light that is both linearly polarized and correctly aligned to one of the two PM fiber's axes. Due to this, setups for coupling light into a PM fiber often include a linear polarizer and some means for rotating the orientation of the input polarization state. This Video Insight demonstrates two methods for aligning linearly polarized input light. The first approach uses a polarimeter, and the second uses a linear polarizer in front of a power sensor. Both approaches require smoothly increasing or decreasing the fiber’s birefringence, which is accomplished during this demonstration by heating or cooling the fiber.
When coupling light into a PM fiber, it is important to first align the system to achieve maximum coupling efficiency, as previously shown for FiberBenches and for fiber collimators. The next step is to use one of the methods demonstrated in this Video Insight to ensure the input light is linearly polarized and oriented parallel with either the slow or the fast axis of the PM fiber. This alignment enables the PM fiber to preserve the input polarization state, since the light travels along only one of the fiber's axes.
Both polarimeter and analyzing polarizer methods measure the PM fiber's optical output. This video shows that better alignment corresponds with the polarimeter data tracing smaller circles around a point on the Poincaré sphere’s equator. These data are shown alongside and compared with measurements of the optical power transmitted through an appropriately oriented linear polarizer. Better alignment corresponds to smaller-amplitude power oscillations. A brief discussion of PM fibers and an introduction to relevant features on the Poincaré sphere are also included.
For additional information about the interaction between light and PM fiber, click here.
Date of Last Edit: May 1, 2023
|
Right Click to Copy Link to this Section |
28 |
Herriott Cell Setup and Configuration (Viewer Inspired)
In a Herriott cell, light reflects multiple times between two concave mirrors. The reflected beams cross the volume between the two mirrors at different angles, tracing out different paths and creating linear, elliptical, or circular spot patterns on the mirrors. To allow the beam to enter and exit the cell, one or both of the mirrors typically has a hole at its center or near its edge. Herriott cells are used in a variety of applications that benefit from folding a long optical path length into a compact space. Gas-absorption spectroscopy is a popular application, since every additional pass of the beam through the sample volume increases the signal-to-noise ratio of the measurement data.
This demonstration begins with a roughly aligned setup, in which one mirror has a hole near its edge and the other has no hole. Both mirrors have the same focal length. A non-polarizing beamsplitter and a pair of irises are used to set the mirror orientations so they are parallel to each other and perpendicular to a line of screw holes in the table. After this procedure is completed, the angular orientations of the mirrors are no longer adjusted. The demonstration then shows how to achieve different reflection patterns on the mirrors by changing the input beam orientation and cell length.
Both the input beam angle and mirror spacing affect the number of reflections the beam experiences before exiting the cell. A special case is when the two mirrors have the same focal length and are separated by a distance equal to the focal length. This configuration always provides six passes through the cell, regardless of the orientation of the input beam. This mirror spacing is used to illustrate the effects of changing the input beam’s pitch and yaw angles, as well as the beam’s X-axis and Y-axis position. In addition, the input beam is aligned parallel to the cell’s optical axis as a starting point. Then, the cell length is adjusted to increase the number of passes through the cell. Further adjustments to the input beam orientation are demonstrated to create linear, elliptical, and circular reflection patterns.
References:
D. Herriott et al., Appl. Opt. 3, 523-526 (1964).
C.G.Tarsitano et al., Appl. Opt. 46, 6923-6935 (2007).
Date of Last Edit: Jul. 14, 2023
|
Right Click to Copy Link to this Section |
29 |
Collimate Light from an LED
Collimating light from an LED or other large, incoherent source can be a surprisingly challenging task. The emitter’s size and the collimating lens’ focal length and numerical aperture (NA) all influence the characteristics of the collimated beam. It can also be hard to know when the lens is positioned optimally. In this video, two lenses with different NAs and focal lengths are used to demonstrate a couple of collimation approaches. In addition, the emerging image of the emitter and other typical features of beams provided by collimating lenses are explored.
Two significant collimated beam properties are divergence and optical power. As shown in this demonstration, when two lenses have the same diameter, more light is collected when the focal length is smaller, since the NA is larger, but at the cost of increased collimated beam divergence. The divergence is also affected by the light emitter’s physical size. Assuming the same lens is used, the collimated beam’s divergence is larger when the emitter is larger.
One consequence of a larger divergence is that the beam’s irradiance (optical power per area) decreases at a faster rate with increasing distance from the lens. Another consequence is that the collimated region is shorter. The collimated region can be described as the part of the beam where rays from across the entire emitter overlap, which is usually close to the lens. With increasing distance from the lens, divergence separates the rays into different bundles, according to their point of origin, revealing an image of the emitter. Seeing an image can be unexpected, since it is not predicted by the thin lens equation and can create unexpected artifacts in an application.
Date of Last Edit: Jan. 12, 2024
|
Right Click to Copy Link to this Section |
30 |
Build a Solar Imaging Telescope with Tracking Capability
Imaging the sun can be dangerous to both people and equipment, but telescopes can be modified to include optical attenuators that reduce the image intensity to safe levels. The further addition of motors and software control allows a solar telescope’s azimuth and altitude positions to be automatically adjusted, enabling continuous tracking of the sun as it moves across the sky. In this video, a refractive solar imaging telescope, which uses a camera as the imaging device and Python code to control the motors, is designed, constructed, and demonstrated. The Python code and detailed instructions are available for download from Thorlabs' GitHub page.
The telescope’s design was constrained by the dimensions, light saturation limits, and response of the camera’s CMOS sensor. The focal length of the lens was chosen to provide the largest image that fit comfortably within the sensor's area. That focal length determined the spacing between the lens and the camera. Optimizing the optical attenuation required first calculating a value providing intensity significantly beneath the sensor’s saturation limit, and then incrementally reducing the attenuation to shorten the camera's exposure time to less than 10 ms.
Tracking capability was implemented using two motorized rotation stages, which were mounted in an orthogonal configuration using a custom 3D-printed bracket, whose design file is also available for download. Testing and rough alignment is performed indoors, and then the telescope is taken outside to demonstrate its ability to image and track the sun.
Date of Last Edit: Apr. 4, 2024
|
Right Click to Copy Link to this Section |
31 |
How Light’s Incident Angle Affects Transmission & Finding Brewster’s Angle
It is common to assume 4% of light reflects from a glass surface. While this rule-of-thumb can be used near normal incidence, the approximation is not appropriate for all incident angles, and it does not provide information about the input polarization state's effect on the reflected and transmitted optical powers. During this demonstration, light reflected from, and transmitted through, a rotating glass window is observed and compared with the results from Fresnel equation modeling. The limits of the 4% rule are investigated, and the polarization dependence of the reflectance and transmittance values are explored.
First s-polarized and then p-polarized input light is incident upon the rotating window, which reveals that the light’s reflectance and transmittance values depend on the input polarization state of the incident beam. (S-polarized light is linearly polarized perpendicular to the plane of incidence and p-polarized light is linearly polarized parallel.) It is shown that there is an angle of incidence at which all incident p-polarized light is transmitted, so that only s-polarized light is reflected. This is called the Brewster’s angle, and an approach is demonstrated to orient the window so that the light is incident at Brewster’s angle.
Linearly polarized input light oriented at 45° to the plane of incidence is also used to demonstrate that, when transmittance and reflectance values for pure s- and p-polarized light are known, it is possible to use these values to predict the values for unpolarized light.
Date of Last Edit: May 7, 2024
|
Right Click to Copy Link to this Section |
32 |
| Posted Comments: | |
aroopkanti bose
(posted 2021-07-15 17:21:51.7) Can you please add a video on SPCM20A/M appln lmorgus
(posted 2021-07-16 09:33:53.0) A response from Laurie at Thorlabs to aroopkanti bose: Thanks for your suggestion! Do you have a specific application in mind for a single photon counter? |
 Products Home
Products Home Video Insights
Video Insights